Use anchoring to lose years off your age

It is well known in psychology that the way a question is asked can strongly influence the answer. For example, if you spin a random number wheel and later have people guess the proportion of United Nations countries that are African, their answers closely follow the number the wheel landed on. The initial random number serves as a reference or anchor for their guesses.

Suppose you wanted people to guess you had a lower age than you really had. One way to do it would be to anchor the question with the numbers 12 and 42 and compare the results. Specifically, when someone asked you what your age was you could tell them,

• I’m really 12 years old, don’t tell my mom and dad I’m talking to strangers
  
• I’m 42 years old but you can’t tell because of my macrobiotic diet based on microfibers

before having them guess your age.

Just for fun I asked 16 people in each anchoring condition to guess my age. The mean age of the people making the guess in the “42” condition was 20.4 years and for the “12” condition it was 20.8. Not much of difference, so any age effect would be solely due to the anchoring effect.

Results
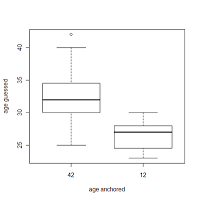
The mean age for the guess in the “42” condition was 32.4, for the “12” condition it was 26.4, here is a boxplot of the respective guesses
To make sure the results were statistically significant I performed a bootstrap calculation with R

Intervals : Level      Normal     95%   ( 3.375,  8.622 )

The bootstrap confidence interval doesn’t contain 0, which means there was indeed a statistically significant anchoring effect and if you want people to think you look younger than you really are, you might want to anchor your age to a ridiculously low number.

Here’s the R code to perform the bootstrap

library(boot)
#The guesses of the girls
guess.42<-c(28,33,40,34,42,25,33,30,31,28,30,30,35,32,35)
guess.12<-c(23,28,26,25,25,30,27,28,28,23,27,28,30,24,24)
D = data.frame(guess.42,guess.12)
samplemean <- function(D, d) {
E=D[d,]
return(mean(E$guess.42)-mean(E$guess.12))
}
b = boot(D, samplemean, R=1000)
print(b)
plot(b)
boot.ci(b)
boxplot(guess.42,guess.12,ylab="age guessed",xlab="age anchored",names=c("42","12"))
#Now we do a t test
t.test(guess.42,guess.12,type="greater")

Note: It was obvious that the people who guessed 23, and above 35, as my age were joking, nonetheless it was interesting that the exaggerated ages they chose in jest were close to the anchor.